Pregunta 25_2010

Para que la expresión

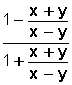
sea positiva, se debe cumplir necesariamente que

A)  xy < 0
B)  x < 0
C)  xy > 0
D)  y < 0
E)  x > y

Área temática: Álgebra

Comentario

En este ítem el alumno debe trabajar con fracciones algebraicas , para ello debe sumar fracciones, factorizar y simplificar el numerador con el denominador de la fracción resultante. Después debe hacer un análisis de la expresión resultante para determinar las condiciones necesarias para que la fracción sea positiva.

Es decir,

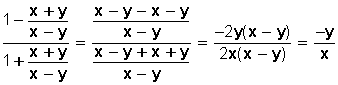
Para que una fracción sea positiva el numerador y el denominador deben serlo, o bien ambos deben ser negativos, luego (fracción negativa) será positiva cuando se cumplen las desigualdades ( ─y > 0 y x > 0 ) o ( ─y < 0 y x < 0 ). Entonces, del primer paréntesis, si ─y > 0 y x > 0 , se tiene que y < 0 y x > 0 , por lo que xy < 0 . Ahora, del segundo paréntesis, si ─y < 0 y x < 0 , se tiene que y > 0 y x < 0 , por lo tanto xy < 0 . Como en ambos casos se llega a que xy < 0 , la clave es la opción A) .

Este ítem resultó muy difícil. Muy pocos alumnos contestaron correctamente, lo cual hace pensar que la gran mayoría no domina a cabalidad el contenido o no están acostumbrados a trabajar con este tipo de preguntas en donde la respuesta no es una expresión sino una condición. Además, requiere que el estudiante haya desarrollado las habilidades de orden superior, como el análisis de situaciones.

El distractor con más preferencias fue C). Quienes se inclinaron por él, posiblemente operaron mal la fracción algebraica ,  entonces asumen que esta fracción es mayor que cero cuando xy > 0.

Fuente Internet:

Publicación oficial del Demre en www.demre.cl